Příklad 33:  Nechť    je regulární zobrazení z  do   a funkce    má spojité parciální derivace do 2. řádu na množině . Pro derivaci složené funkce V podle proměnných   platí

                                               

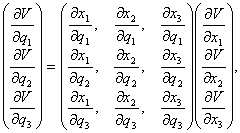
kde

   

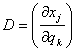
je nenulový Jacobián regulárního zobrazení. Pokud by byly řádky matice D  ortonormální vektory, potom by inverzní matice k matici D  byla . Znormujeme proto řádkové vektory Jacobiánu. Normy (nazývané Laméovy koeficienty) označíme , je

                                                 .

 

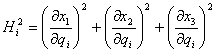Potom

                                

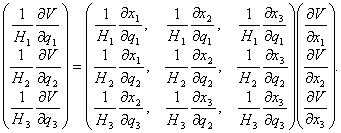
Pro parciální derivace funkce V platí

                                   

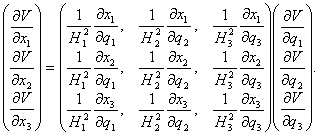
1.      Polární souřadnice: , .

Laméovy koeficienty:  

         

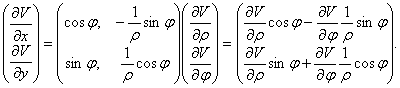
Napravo je gradient v polární soustavě souřadnic , kterou je třeba otočit do kartézské  báze, tj. vynásobit zleva maticí přechodu

                                                 ,

potom

                                        ,

 

  1. Sférické souřadnice:  ,

     

 Laméovy koeficienty:  

                      

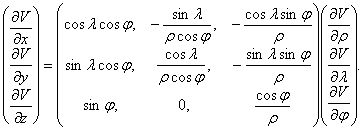
              Matice přechodu od sférických souřadnic ke kartézským je 

             

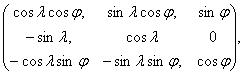
              tou násobíme vektor pravé strany zprava, tj.

                                         

 

Další příklad