Pomoc při studiu matematiky

Užitečné vzorce a návody

4. Trojúhelník

Pythagorova věta

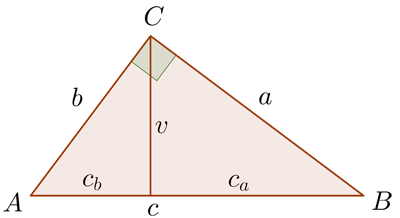
V pravoúhlém trojúhelníku platí \begin{eqnarray} a^2+b^2 \; = \; c^2 \end{eqnarray}

Euklidovy věty

V pravoúhlém trojúhelníku platí \begin{eqnarray} c_a\cdot c_b & = & v_c^2 \qquad\qquad\text{Euklidova věta o výšce} \\ c\cdot c_a & = & a^2 \qquad\qquad\text{Euklidova věta o odvěsně}\ a \\ c\cdot c_b & = & b^2 \qquad\qquad\text{Euklidova věta o odvěsně}\ b \end{eqnarray}

Kosinová věta

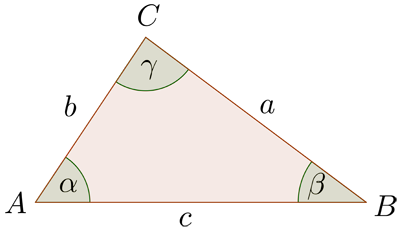
V libovolném trojúhelníku platí \begin{eqnarray} a^2 & = & b^2 + c^2 - 2bc\cos \alpha \\ b^2 & = & c^2 + a^2 - 2ca\cos \beta \\ c^2 & = & a^2 + b^2 - 2ab\cos \gamma \end{eqnarray}

Sinová věta

V libovolném trojúhelníku platí \begin{eqnarray} \frac{a}{\sin\alpha} \;\; = \;\; \frac{b}{\sin\beta} \;\; = \;\; \frac{c}{\sin\gamma} \end{eqnarray}

Zpět